Pohyb po kružnici - online puzzle
Online puzzle Pohyb po kružnici
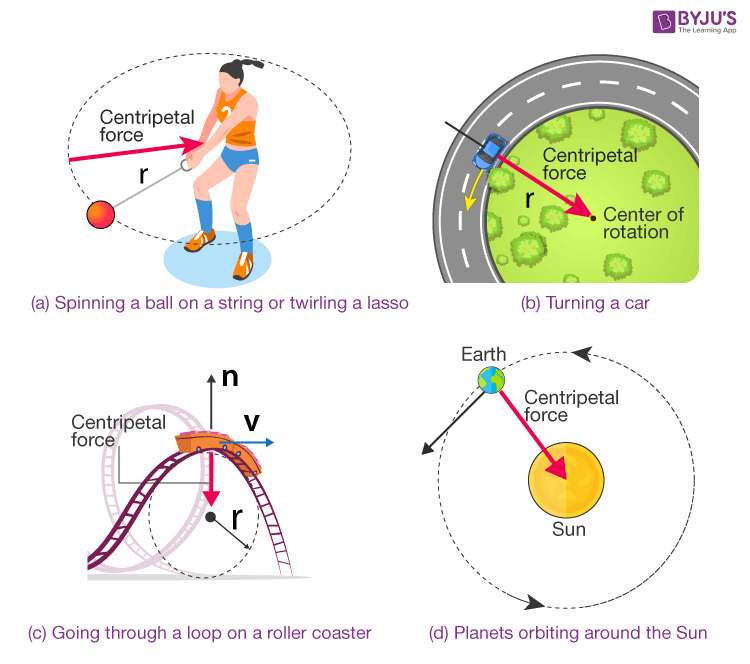
Pohyb po kružnici
Pohyb po kružnici je pohyb (hmotného bodu), jehož trajektorií je kružnice.
Poloha hmotného bodu při pohybu po kružnici (pohyb se středem v počátku soustavy souřadnic):
Zápis v polární soustavě souřadnic
r
=
k
o
n
s
t
.
{\displaystyle r=\mathrm {konst.} }
φ
=
φ
(
t
−
t
0
)
+
φ
0
{\displaystyle \varphi =\varphi (t-t_{0})+\varphi _{0}}
lze přepsat do kartézské soustavy souřadnic:
x
=
r
cos
(
φ
(
t
−
t
0
)
+
φ
0
)
{\displaystyle x=r\cos(\varphi (t-t_{0})+\varphi _{0})}
y
=
r
sin
(
φ
(
t
−
t
0
)
+
φ
0
)
{\displaystyle y=r\sin(\varphi (t-t_{0})+\varphi _{0})}
Konstantní r představuje poloměr trajektorie, φ(t) je tzv. úhlová dráha, což je úhel, který za čas t opíše spojnice středu dráhy a pohybujícího se bodu (průvodič), φ0 je úhlová dráha v počátečním čase t0. Při pohybu se s časem mění pouze úhel φ, poloměr dráhy je konstantní.
Dráha pohybu po kružnici
Rozlišuje se obvodová dráha a úhlová dráha.
Obvodová dráha s je vzdálenost, kterou urazí hmotný bod během pohybu po obvodu kružnice.
Úhlová dráha φ je úhel, který urazí průvodič hmotného bodu během pohybu.Mezi úhlovou dráhou a obvodovou dráhou je vztah (r je poloměr kružnice):
φ
=
s
r
{\displaystyle \varphi ={\frac {s}{r}}}