Послідовність Фібоначчі - онлайн головоломки


Онлайн пазл Послідовність Фібоначчі
Послідовність Фібоначчі
Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — у математиці числова послідовність
F
n
,
{\displaystyle {F_{n}},}
задана рекурентним співвідношенням другого порядку
F
1
=
1
,
F
2
=
1
,
F
n
+
2
=
F
n
+
F
n
+
1
,
n
=
1
,
2
,
3
,
…
,
{\displaystyle F_{1}=1,F_{2}=1,F_{n+2}=F_{n}+F_{n+1},n=1,2,3,\ldots ,}
F
1
=
1
,
F
2
=
1
,
F
3
=
2
,
F
4
=
3
,
F
5
=
5
,
F
6
=
8
,
F
7
=
13
,
F
8
=
21
,
{\displaystyle F_{1}=1,F_{2}=1,F_{3}=2,F_{4}=3,F_{5}=5,F_{6}=8,F_{7}=13,F_{8}=21,\,}
і т. д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях — комбінаторних, числових, геометричних.
Простіше кажучи, перші два члени послідовності — одиниці, а кожний наступний — сума значень двох попередніх чисел:
1
,
1
,
2
,
3
,
5
,
8
,
13
,
21
,
34
,
55
,
89
,
144
,
…
{\displaystyle 1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}
Часто, особливо в сучасному вигляді, послідовність доповнюється ще одним початковим членом:
0
,
1
,
1
,
2
,
3
,
5
,
8
,
13
,
21
,
34
,
55
,
89
,
144
,
…
{\displaystyle 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}
.За визначенням, перші два числа в послідовності Фібоначчі є або 1 і 1, або 0 і 1, залежно від обраного початку послідовностей, а кожне наступне число є сумою двох попередніх.
В математичних термінах послідовність чисел Фібоначчі Fn визначається як рекурентне співвідношення
F
n
=
F
n
−
1
+
F
n
−
2
,
{\displaystyle F_{n}=F_{n-1}+F_{n-2},}
із початковими значеннями
F
1
=
1
,
F
2
=
1
{\displaystyle F_{1}=1,\;F_{2}=1}
або
F
0
=
0
,
F
1
=
1.
{\displaystyle F_{0}=0,\;F_{1}=1.}
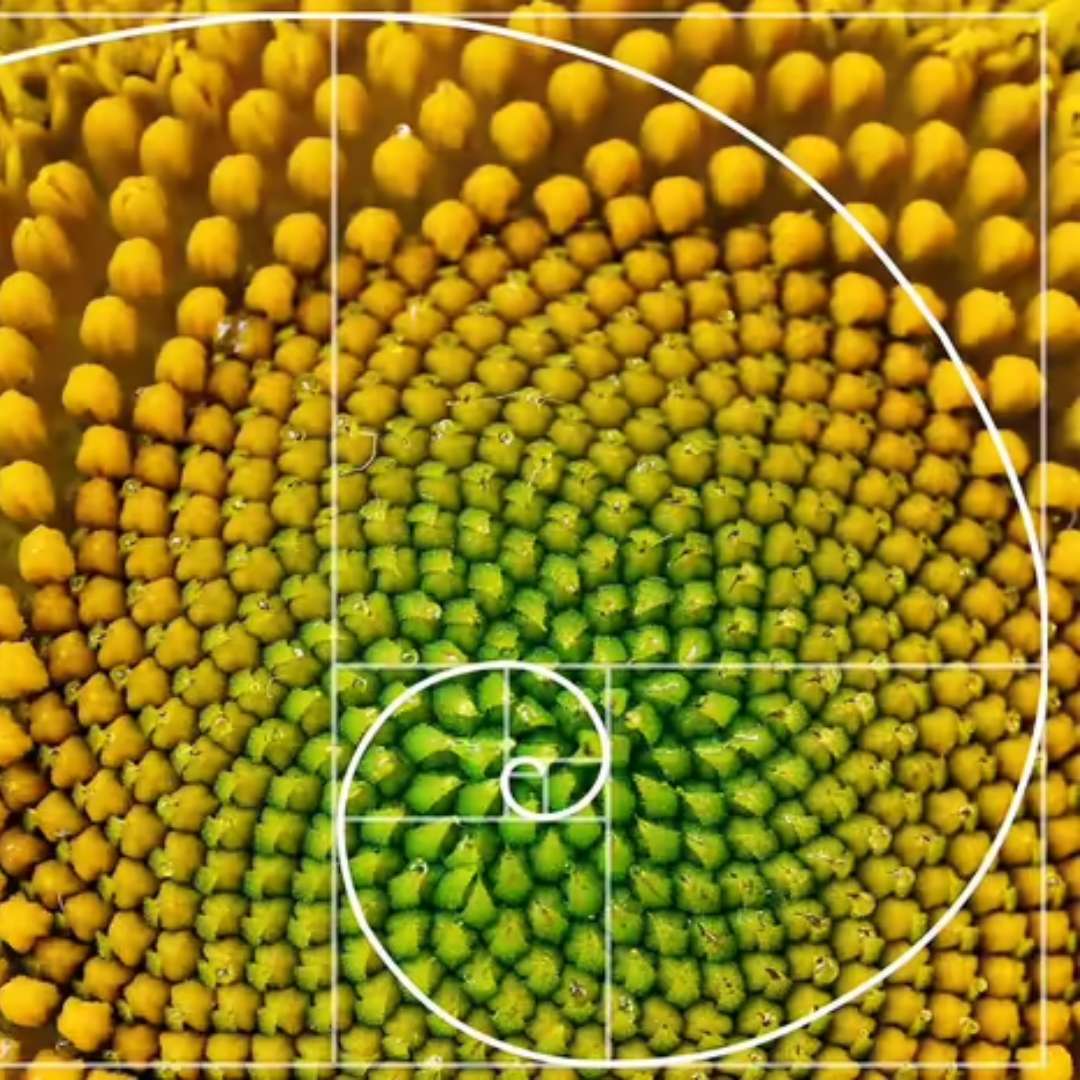
У природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 — у дуба, 3/8 — у тополі і груші, 5/13 — у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.
Послідовність названа на честь математика XIII століття Леонардо Фібоначчі з Пізи. Його 1202 книга — Книга абака — представила цю послідовність спільноті західноєвропейських математиків, хоча така послідовність вже була описана раніше як числа Вараханка в індійській математиці. Послідовність, описана в «Книзі абака», починалася з F1 = 1.