Slope - online puzzles











































Online puzzle Slope
Slope
In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but its earliest use in English appears in O'Brien (1844) who wrote the equation of a straight line as "y = mx + b" and it can also be found in Todhunter (1888) who wrote it as "y = mx + c".Slope is calculated by finding the ratio of the "vertical change" to the "horizontal change" between (any) two distinct points on a line. Sometimes the ratio is expressed as a quotient ("rise over run"), giving the same number for every two distinct points on the same line. A line that is decreasing has a negative "rise". The line may be practical – as set by a road surveyor, or in a diagram that models a road or a roof either as a description or as a plan.
The steepness, incline, or grade of a line is measured by the absolute value of the slope. A slope with a greater absolute value indicates a steeper line. The direction of a line is either increasing, decreasing, horizontal or vertical.
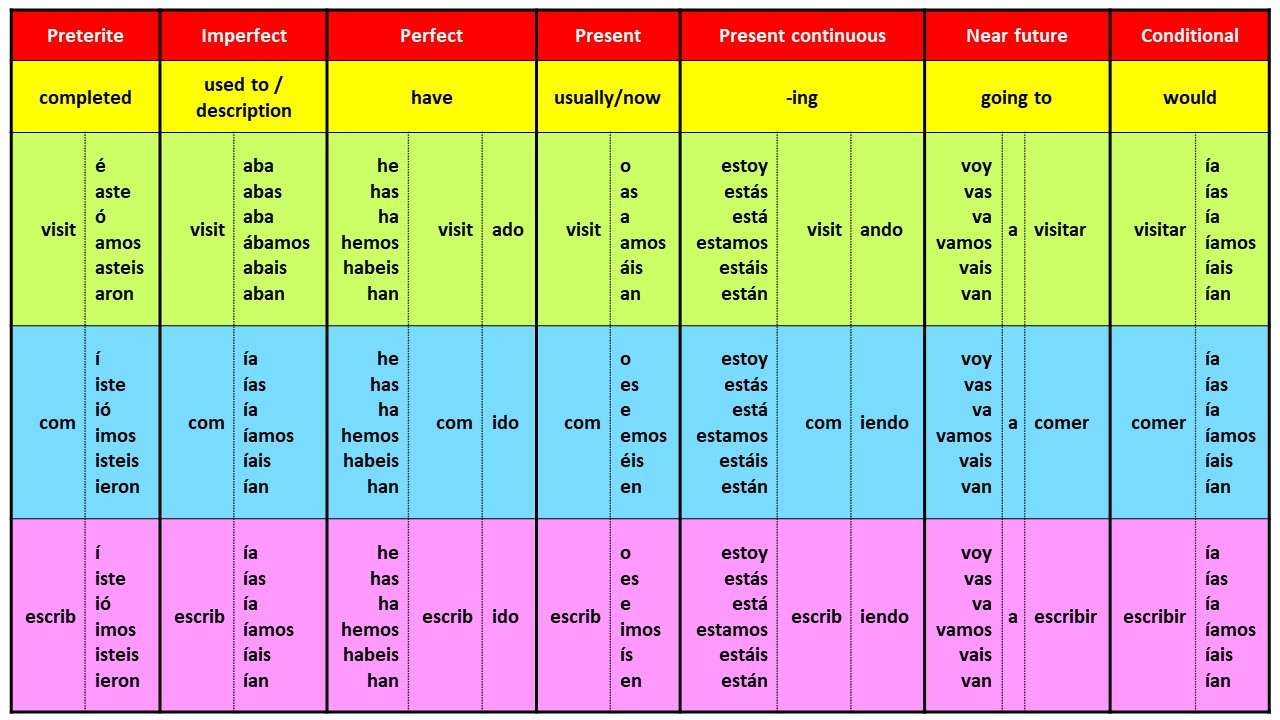
A line is increasing if it goes up from left to right. The slope is positive, i.e.
m
>
0
{\displaystyle m>0}
.
A line is decreasing if it goes down from left to right. The slope is negative, i.e.
m
<
0
{\displaystyle m<0}
.
If a line is horizontal the slope is zero. This is a constant function.
If a line is vertical the slope is undefined (see below).The rise of a road between two points is the difference between the altitude of the road at those two points, say y1 and y2, or in other words, the rise is (y2 − y1) = Δy. For relatively short distances, where the Earth's curvature may be neglected, the run is the difference in distance from a fixed point measured along a level, horizontal line, or in other words, the run is (x2 − x1) = Δx. Here the slope of the road between the two points is simply described as the ratio of the altitude change to the horizontal distance between any two points on the line.
In mathematical language, the slope m of the line is
m
=
y
2
−
y
1
x
2
−
x
1
.
{\displaystyle m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}.}
The concept of slope applies directly to grades or gradients in geography and civil engineering. Through trigonometry, the slope m of a line is related to its angle of inclination θ by the tangent function
m
=
tan
(
θ
)
{\displaystyle m=\tan(\theta )}
Thus, a 45° rising line has a slope of +1 and a 45° falling line has a slope of −1.
As a generalization of this practical description, the mathematics of differential calculus defines the slope of a curve at a point as the slope of the tangent line at that point. When the curve is given by a series of points in a diagram or in a list of the coordinates of points, the slope may be calculated not at a point but between any two given points. When the curve is given as a continuous function, perhaps as an algebraic expression, then the differential calculus provides rules giving a formula for the slope of the curve at any point in the middle of the curve.
This generalization of the concept of slope allows very complex constructions to be planned and built that go well beyond static structures that are either horizontals or verticals, but can change in time, move in curves, and change depending on the rate of change of other factors. Thereby, the simple idea of slope becomes one of the main basis of the modern world in terms of both technology and the built environment.